4. Indistinguishable function
Given a Lipschitz function f on a compact domain \alpha, a positive real number \varepsilon, and an element of \alpha c, we construct a new Lipschitz function \tilde{f} such that f = \tilde{f} outside of the ball centered at c with radius \varepsilon/2, and such that the maximum value of \tilde{f} is inside this ball and is strictly greater than the maximum value of f.
4.1. Expression
We define the function \tilde{f} as follows:
\tilde{f}(x) \triangleq \begin{cases}
f (x) + 2 \cdot \left(1 - \frac{\|x - c\|}{\varepsilon / 2} \right) \cdot (\max_{x \in \alpha} f(x) - \min_{x \in \alpha} f(x) + 1) & \text{if } x \in B(c, \varepsilon / 2) \\
f (x) & \text{otherwise}
\end{cases}
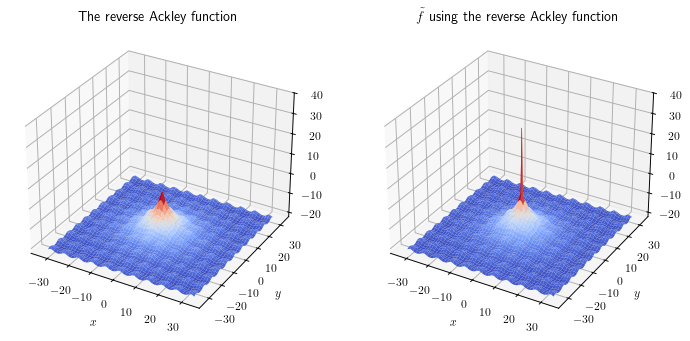
Here is a visualization of this expression using the reverse Ackley function.
noncomputable def f_tilde (ε : ℝ) (x : α) :=
if x ∈ ball c (ε/2) then
f x + 2 * ((1 - (dist x c) / (ε/2)) * (fmax hf - fmin hf + 1))
else f x4.2. Lipschitz property
We show that \tilde{f} is Lipschitz continuous. The proof relies on the fact that \tilde{f} is a cases function of two Lipschitz functions that are equal on the frontier of the ball B(c, \varepsilon / 2).
lemma f_tilde_lipschitz {ε : ℝ} (ε_pos : 0 < ε) : Lipschitz (hf.f_tilde c ε) := α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ Lipschitz (hf.f_tilde c ε)
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ ∀ a ∈ sphere c (ε / 2), 2 * ((1 - dist a c / (ε / 2)) * (fmax hf - fmin hf + 1)) = 0α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ Lipschitz fun a => 2 * ((1 - dist a c / (ε / 2)) * (fmax hf - fmin hf + 1))
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ ∀ a ∈ sphere c (ε / 2), 2 * ((1 - dist a c / (ε / 2)) * (fmax hf - fmin hf + 1)) = 0 α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εa:αha:a ∈ sphere c (ε / 2)⊢ 2 * ((1 - dist a c / (ε / 2)) * (fmax hf - fmin hf + 1)) = 0
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εa:αha:a ∈ sphere c (ε / 2)⊢ 2 * ((1 - ε / 2 / (ε / 2)) * (fmax hf - fmin hf + 1)) = 0
suffices h : ε / 2 / (ε / 2) = 1 α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εa:αha:a ∈ sphere c (ε / 2)h:ε / 2 / (ε / 2) = 1 := ?m.14733⊢ 2 * ((1 - ε / 2 / (ε / 2)) * (fmax hf - fmin hf + 1)) = 0
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εa:αha:a ∈ sphere c (ε / 2)h:ε / 2 / (ε / 2) = 1 := ?m.14733⊢ 2 * ((1 - 1) * (fmax hf - fmin hf + 1)) = 0
All goals completed! 🐙
All goals completed! 🐙
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ Lipschitz fun a => 2 * ((1 - dist a c / (ε / 2)) * (fmax hf - fmin hf + 1)) α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ Lipschitz fun a => dist a c / (ε / 2)
All goals completed! 🐙
4.3. Maximum of \tilde{f}
One can show that \tilde{f}(c) is strictly greater than the maximum of f (see max_f_lt_f_tilde_c). Hence, by transitivity, the maximum of \tilde{f} is strictly greater than the maximum of f.
lemma max_f_lt_max_f_tilde {ε : ℝ} (ε_pos : 0 < ε) :
fmax hf < fmax (hf.f_tilde_lipschitz c ε_pos) :=
suffices h : fmax hf < hf.f_tilde c ε c from
lt_of_le_of_lt' (compact_argmax_apply (hf.f_tilde_lipschitz c ε_pos).continuous c) h
hf.max_f_lt_f_tilde_c c ε_pos
Finally, we show that the maximum of \tilde{f} is attained in the ball B(c, \varepsilon / 2).
lemma max_f_tilde_in_ball {ε : ℝ} (ε_pos : 0 < ε) :
compact_argmax (hf.f_tilde_lipschitz c ε_pos).continuous ∈ ball c (ε/2) := α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ compact_argmax ⋯ ∈ ball c (ε / 2)
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εx':α := compact_argmax ⋯⊢ x' ∈ ball c (ε / 2)
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εx':α := compact_argmax ⋯h_contra:x' ∉ ball c (ε / 2)⊢ False
have : fmax (hf.f_tilde_lipschitz c ε_pos) ≤ fmax hf := α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < ε⊢ compact_argmax ⋯ ∈ ball c (ε / 2)
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εx':α := compact_argmax ⋯h_contra:x' ∉ ball c (ε / 2)⊢ f (compact_argmax ⋯) ≤ f (compact_argmax ⋯)
All goals completed! 🐙
α:Type u_1inst✝³:NormedAddCommGroup αinst✝²:CompactSpace αinst✝¹:Nonempty αf:α → ℝhf:Lipschitz fc:αinst✝:NormedSpace ℝ αε:ℝε_pos:0 < εx':α := compact_argmax ⋯h_contra:x' ∉ ball c (ε / 2)this✝:fmax ⋯ ≤ fmax hf :=
Eq.mpr (id (congrArg (fun x => x ≤ f (compact_argmax (fmax._proof_1 hf))) (f_tilde_apply_out hf c h_contra)))
(compact_argmax_apply (continuous hf) x')this:fmax hf < fmax ⋯ := max_f_lt_max_f_tilde hf c ε_pos⊢ False
All goals completed! 🐙